[Up]   ホーム

Guile基礎／グラフアルゴリズムの基礎

変更履歴

• 2022.4.28：初出

概 要

• プログラミング学習の題材として，各種アルゴリズムの実装を試してみようと思います． とりあえず，グラフのアルゴリズムを実装してみようと思います． おもな目的はベクタやレコードに少しでも馴染むことです． このノートは筆者が利用するグラフのデータ構造について説明します．
• 以下では，グラフに関して次のような用語や記法を使用します．
  • 任意のグラフを $G = (V,E)$ で表します． ここで，$V$ は $G$ の頂点（vertex）の集合を表し，$E$ は$G$ の辺（edge）の集合を表します．
  • 頂点 $u$ と $v$ を結ぶ無向辺を $\{u,v\}$ で表し， 有向辺を $(u,v)$ で表すことにします．
  • $n$個の頂点からなるグラフの各頂点は $0 \sim n-1$ の番号によって表現します． 従って，$n$頂点グラフの頂点集合は $V = \{0,1, ..., n-1\}$ となります．

• 筆者は Debian 11(bullseye) を使っていて，Guile は Debian 11 が配布するパッケージを使っています．そのバージョンは 3.0.5 です． ちなみに，2022.3.1時点の最新版は 3.0.8 です．

目 次

• グラフのデータ構造
  • グラフのレコード型
  • グラフレコードの手続き
  • モジュール
• 具体例
  • 辺に重みのない無向グラフの具体例
  • 辺重み付き有向グラフの具体例

参考資料

• Guile
  • GNU Guile Reference Manual（最新版）
    [6.7.4 Optional Arguments]
  • GNU Guile Reference Manual, Edition 3.0.5, revision 1 (for Debian 11)
  （注）Guileのマニュアルは常に最新版を参照しています．少し困ったことに，バージョン番号の3桁目が変化しただけでも，マニュアルの編成が大きく変化することがあります．実際，3.0.5 と 3.0.8 はかなり違っています．Guile のバージョンが上がることによって，上記のマニュアルの参照（特に，節番号）は古くなるかも知れません．ただ，リンク先の名前に節番号は入っていないので，リンクが途切れることはないだろうと期待します．それから，現在使用中のシステム（例えば，Debian 11 の 3.0.5）については，info形式のオンラインマニュアルが参照できます．
• Scheme
  • small.r7rs.org： Revised⁷ Report on the Algorithmic Language Scheme（略号：R⁷RS）
    英語版 日本語版
  • R. Kent Dybvig: The Scheme Programming Language, Fourth Edition, 2009.（略号：TSPL）
  • www.r6rs.org ：Revised⁶ Report on the Algorithmic Language Scheme （略号：R⁶RS） 英語版 日本語版

• このノートはMathJaxを使用しています．
  • 奥村晴彦先生のMathJaxのページ
  • MathJax本家

グラフのデータ構造

グラフのレコード型

グラフを扱うためのデータ構造として，以下のように定義されるレコードを使用します．

(define-record-type <graph>
  (make-graph number-of-nodes   ;; 頂点数
              number-of-edges   ;; 辺数
              type              ;; 無向（'undirected） か 有向（'directed）
              root              ;; グラフの根
              adj)              ;; 隣接リスト構造
  graph?
  (number-of-nodes get-num-nodes  set-num-nodes!)
  (number-of-edges get-num-edges  set-num-edges!)
  (type            get-type       set-type!)
  (root            get-root       set-root!)
  (adj             get-adj-vector set-adj-vector!))

ここで：

• type はグラフのタイプ（無向グラフか有向グラフ）を保持するフィールドです． 無向グラフのときには 'undirected を指定し， 有向グラフのときには 'directed を指定します．
• root はグラフの根を保持するためのフィールドです． おもに根付き有向木を扱うときに使用します．
• adj は隣接リストを保持するためのベクタです． 頂点数（number-of-nodes）を$n$とするとき， このベクタは$n$個の成分を持ち，第$u$番目の成分は頂点$u$の隣接情報を保持していて， 次のようなリストに束縛されます．
  ( ($v_1$ . $w_1$) ($v_2$ . $w_2$) ... ($v_k$ . $w_k$) )
  ここで，$v_1$〜$v_k$ は頂点$u$の隣接頂点を表し，各$w_i$は$u$と$v_i$を結ぶ辺の重みを表しています．ただし，有向グラフの場合，頂点$u$を始点とする有向辺の終点とその有向辺の重みを保持します．
• 以後，上記のペア ($v_i$ . $w_i$) のことを頂点$u$の隣接点ペアと呼び， 上記のリストを頂点$u$の隣接リストと呼ぶことにします． さらに，adj のことを隣接リストベクタと呼ぶことにします．
• 辺の重みは整数値とします．辺に重みのないグラフを扱うときには，辺の重みを便宜的に #f に設定します．

以後，このレコードをグラフレコードと呼ぶことにします．

グラフレコードの手続き

上記の各フィールドのアクセッサやモディファイアに加えて， グラフレコードに関して次のようなマクロを利用します． これらをマクロにしているのは，今後の実験において100万頂点や1000万頂点のグラフを扱うつもりなので，手続き呼び出しのオーバーヘッドを少しでも減らすためです．

;; G が無向グラフのとき #t を返し，有向グラフのとき #f を返す．
(define-syntax-rule (undirected? G) 
  (eq? (get-type G) 'undirected))

;; G が有向グラフのとき #t を返し，無向グラフのとき #f を返す．
(define-syntax-rule (directed? G) 
  (eq? (get-type G) 'directed))

;; 頂点uの隣接リスト adj[u] に隣接点ペア (v . weight) を追加する．
(define-syntax-rule (add-directed-edge adj u v weight)
  (vector-set! adj u (cons (cons v weight) (vector-ref adj u))))

;; 頂点uの隣接リスト adj[u] に隣接点ペア (v . weight) を追加し，
;; 頂点vの隣接リスト adj[v] に隣接点ペア (u . weight) を追加する．
(define-syntax-rule (add-undirected-edge adj u v weight)
  (begin 
    (vector-set! adj u (cons (cons v weight) (vector-ref adj u)))
    (vector-set! adj v (cons (cons u weight) (vector-ref adj v)))))

これらに加えて，これ以後の実行例の中で次のようなユーティリティも使用します．

;; グラフGの隣接リストベクタを適当な形式で表示する．
(define* (show-graph G #:optional (print-neighbors #t))
   ...... 詳細略 ......
)

;; Graphvizを利用してグラフGの画像データを生成する．
(define (make-graphviz G fname)
   ...... 詳細略 ......
)

モジュール

グラフレコードの定義と各種手続きをまとめて adjlist という名前のモジュールにしています．そのため，今後の実行例では， 上記の定義や手続きを使うためにこのモジュールを次のようにロードします．

(use-modules (adjlist))

このモジュールは ajdlist.scm にあります．

具体例

辺に重みのない無向グラフの具体例

以下の gen-graph は辺に重みのない$n$頂点の無向グラフを適当に生成します．以下の2番目のループは次のような計算を$2 \times n$回繰り返します．

1. 頂点$u$と$v$の組をランダムに生成します．
2. $u\not=v$かつ辺$\{u,v\}$がまだ生成されていないとき， 辺$\{u,v\}$を隣接リストベクタ adj に登録します． そうでないときには何もしません．

;; ugraph-sample.scm

(add-to-load-path (getcwd))
(use-modules (adjlist))

(set! *random-state* (random-state-from-platform))

(define (gen-ugraph n)
  (define adj (make-vector n '()))
  (define nedges 0)
  (define (ecode u v) (+ (* n u) v))
  (define selected (make-bitvector (* n n) #f))
  (let loop ((u 0))
    (when (< u n)
      (bitvector-set-bit! selected (ecode u u))
      (loop (1+ u))))
  (define ntrials (* 2 n))
  (let loop ((k 0) (u (random n)) (v (random n)))
    (when (< k ntrials)
      (when (bitvector-bit-clear? selected (ecode u v))
        (add-undirected-edge adj u v #f)
        (bitvector-set-bit! selected (ecode u v))
        (bitvector-set-bit! selected (ecode v u))
        (set! nedges (1+ nedges)))
      (loop (1+ k) (random n) (random n))))
  (make-graph n nedges 'undirected 0 adj))

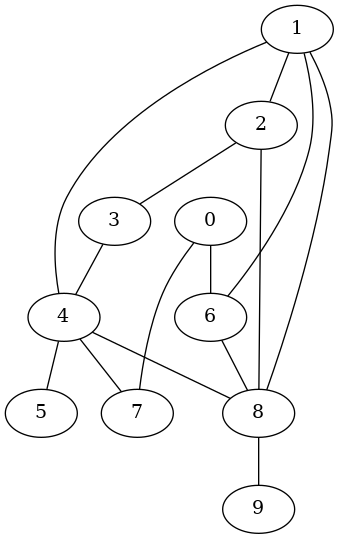
以下の実行例は$10$頂点の無向グラフを生成していて， 隣接リストベクタには14本の辺が登録されています． この例の場合，根は意味を持ちません． 右側の図は Gaphviz を使って生成したものです．

辺重み付き有向グラフの具体例

以下の gen-digraph も前述した手続きとほぼ同じ処理を行っています． 違いは，有向グラフを生成しているうこと，1以上10未満の整数をランダムに生成して辺の重みにしていることです．

;; digraph-sample.scm

(add-to-load-path (getcwd))
(use-modules (adjlist))

(set! *random-state* (random-state-from-platform))

(define (gen-digraph n)
  (define adj (make-vector n '()))
  (define nedges 0)
  (define (random-weight lb ub) (+ lb (random (- ub lb))))
  (define (ecode u v) (+ (* n u) v))
  (define selected (make-bitvector (* n n) #f))
  (let loop ((u 0))
    (when (< u n)
      (bitvector-set-bit! selected (ecode u u))
      (loop (1+ u))))
  (define ntrials (* 2 n))
  (let loop ((k 0) (u (random n)) (v (random n)))
    (when (< k ntrials)
      (when (bitvector-bit-clear? selected (ecode u v))
        (add-directed-edge adj u v (random-weight 1 10))
        (bitvector-set-bit! selected (ecode u v))
        (set! nedges (1+ nedges)))
      (loop (1+ k) (random n) (random n))))
  (make-graph n nedges 'directed 0 adj))

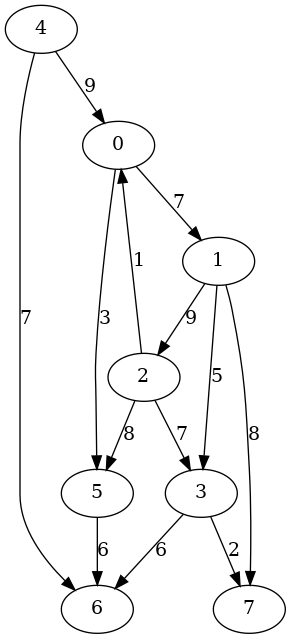
以下の実行例は8頂点の辺重み付き有向グラフを生成しています． この例の場合も根（root）は意味を持ちません．

(おしまい)